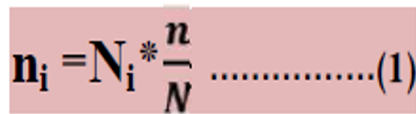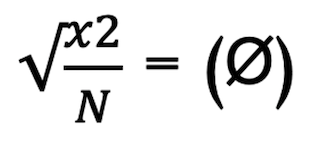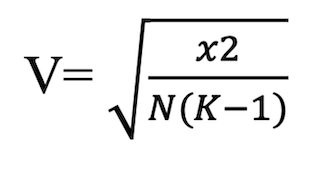مقدمة
يُعتبر أسلوب التحليل الإحصائي من الأساليب التي يتبعها الباحثون في دراسة الظواهر الاجتماعية، حيث يُعد التحليل الإحصائي عملية يتم من خلالها تحضير وتجهيز البيانات المرتبطة بالبحث العلمي، وتتّم عمليّة تحليل البيانات من خلال اتّباع عدد من الطرق الرياضيّة والمنطقيّة قصد الوصول إلى النتائج المرجوة، وقد عرفه بعض العلماء بأنه عبارة عن عملية يتم من خلالها شرح صفات ومعالم مجتمع ما، ولكي يصل الباحث إلى هذه الصفات لابد من إجراء دراسة مجتمع البحث من خلال أخذ عيّنة منه ليتّم دراستها وتعميم نتائجها، إضافة الى تطبيق الاختبارات والفروض الاحصائيّة وبناء الجداول البسيطة والمركبة، ثم تحليلها وقراءتها واستخلاص النتائج منها، وعليه فإننا من خلال هذه الورقة البحثية سنحاول الإجابة على التساؤلات الآتية : ما هي أنواع العينات التي تستخدم في البحوث العلمية ؟ وما هي أنواع الاختبارات الإحصائية؟ وما هي القواعد الواجب اتباعها في قراءة الجداول الإحصائية؟
1. مفاهيم ومصطلحات الدراسة
1.1.مفهوم التحليل الاحصائي
التحليل الإحصائي هو العلمية التي يقوم الباحث من خلالها بجمع البيانات العلميّة وتنظيمها وتحليلها واستخراج معلومات تفيد البحث العلمي من خلالها، بحيث تكون هذه المعلومات جديدة وذات فائدة قيّمة. كما يُعرف التحليل الإحصائي أيضا بأنه العمليّة التي يقوم الباحث من خلالها بالحديث عن مجتمع ما، وشرح صفاته وتحديد المميزات التي تميّزه عن باقي المجتمعات، ولكي يصل الباحث اليها، عليه أن يقوم بأخذ عيّنة منه، لكي يُجري عليها دراسة وفق أسس علميّة، ويستخرج منها الصفات التي يمكن تعميمها على المجتمع، وبالتالي تحديد صفاته المميّزة، وتظهر أهميّته فيما يلي :
-
تساعد الباحثين للوصول إلى النتائج التي يسعون إليها، والتي تكون واضحة وعلى درجة معيّنة من الدقّة والوضوح.
-
ولو لم يُوجد التحليل الاحصائي لتحيّر الباحثون من الكم الكبير من البيانات التي يتّم جمعها والمتوّفرة لدى مختلف الهيئات والمؤسسات في كيفية استغلالها ومعالجتها والاستفادة منها. (أماني موسى 2007: 7)
2.1. أساليب جمع البيانات
تُجمع البيانات الإحصائية عند دراسة صفة ما أو صفات معيّنة لمجتمع بحث ما، بأحد الاسلوبين التاليين:
-
أسلوب الحصر الشامل : وفيه تُجمع البيانات عن كل مفردة من مفردات المجتمع، ويتطلب هذا الأسلوب وفرة في الوقت والمال والمجهود الفنيّ وتزداد هذه المتطلبات وتتضاعف كلما ازداد حجم المجتمع (عدد أفراد المجتمع) وهذا الأسلوب لا يُتّبع عادة إلاّ في حالة التعدادات التي تُجريها الدول وتدعمها بإمكانيات ضخمه مثل تعدادات السكان والتعدادات الصناعيّة والزراعيّة.
-
أسلوب المعاينة :يتّم جمع البيانات عن جزء من مفردات المجتمع يُختار بطريقة أو بأخرى ويُطلق عليه عينة (Echantillon) بعد ذلك يتّم تعميم نتائج الدراسة على المجتمع بأكمله،ويُقصد بأسلوب العيّنة دراسة خصائص المجتمع من خلال دراسة عيّنة مسحوبة منه، ويعتمد نجاح هذا الأسلوب على أن تحمل العيّنة أقصى درجة من دقّة التمثيل للمجتمع المأخوذة منه.
-
المعاينة والمصطلحات المرتبطة بها :بعد بيان دراسة أساليب جمع البيانات لا بد من تعريف بعض المصطلحات الخاصة بالمعاينة والمتمثلة فيما يلي:
-
المجتمع: المجتمع أو المجتمع الاحصائي هو كل الوحدات المراد دراستها بغرض تعميم النتائج. وينبغي الاشارة الى أنّ عملية تحديد المجتمع هي عمليّة نسبيّة ترتبط بالبحث وأهدافه ومشكلته، وهذا ما سنُوّضحه لاحقا.
-
العيّنة: العيّنة هي جزء من المجتمع الذي يقوم الباحث بإجراء الدراسة عليه، ولا بد أن يكون هذا الجزء مُعبرا عن نفس خصائص وصفات الكل،ولا يتّم اجراء هذا إلاّ وفق قواعد خاصّة لكي تمثل المجتمع تمثيلًا صحيحًا.
-
الوحدة الإحصائيّة: هي عبارة عن جزء من نظام محدد يتّم عن طريق اختيار الوحدات المتعلقة بالدراسة، إذ أنّ أي دراسة علميّة احصائيّة ترتكز بشكل اساسيّ على ملاحظة صفات الوحدات المؤلفة لمجتمع احصائي، لذلك يتحتّم قبل القيام بأيّ دراسة تحديد المعنى المُراد من الوحدة الإحصائيّة وقد تكون هذه الاخيرة انسانا أو ظاهرة ما، كما قد تكون مؤسسة أو مهنة.
-
المعاينة : هي عبارة عن الطريقة أو التقنية أو الاُسلوب الذي يتّم بموجبه اختيار عيّنة ملائمة لتحديد خصائص او مواصفات معيّنة للخروج باستنتاجات عن المجتمعات، حيث تستخدم بشكل مستمر في البحوث والدراسات لقدرتها على توفير مجموعة من الفوائد منها( توفير المال، الوقت ودقة بيانات العيّنة) مقارنة مع دراسة جميع أفراد مجتمع الدراسة.
2. أقسام العينات
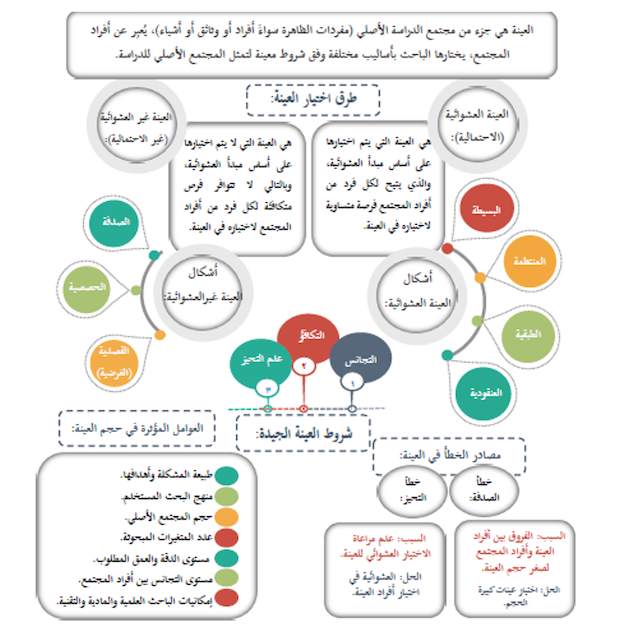
تنقسم العيّنات عادة إلى قسمين رئيسيين وهما عينات عشوائية وعينات غير عشوائية، وفيما يلي تفصيل لكل قسم منها وفق الشكل التالي:
الشكل رقم 1 : أنواع وخطوات اختيار العيّنة
المصدر : https://twitter.com/saudiacademics/status/1117969968190551129
1.2. العيّنات العشوائيّة(الاحتماليّة)
هي العيّنات التي يتّم اختيار مفرداتها وفقا لقواعد الاحتمالات، بمعنى آخر هي التي يتّم انتقاء مفرداتها من مجتمع الدراسة بطريقة عشوائيّة حيث يتّم الاختيار باستخدام أساليب معيّنة تلعب الصدفة خلالها الدور الأول في اختيار المفردة ولكن بشرط أن يتحقق لجميع المفردات احتمال ثابت ومحدد للاختيار، بهدف تجنب التحيّز الناتج عن اختيار المفردات، ومن أهم أنواع العيّنات الاحتماليّة ما يلي:العيّنة العشوائية البسيطة، العيّنة العشوائيّة المنتظمة العيّنة العشوائيّة الطبقيّة والعيّنة العنقوديّة (المتعددة المراحل) ( عبيدات 1998: 111)
1.1.2. العيّنة العشوائيّة البسيطة
يُقصد بالعيّنة العشوائيّة البسيطة تلك العيّنة التي تُؤخذ بطريقة عشوائيّة على أساس إعطاء فرص متكافئة لجميع أفراد المفردات الإحصائيّة ويتم الحصول عليها بإجراء قُرعة لاختيار أفرادها بطريقة تضمن الحظوظ نفسها في الاختيار أو الانتقاء لجميع أفراد المجتمع. فمثلا إذا كان عدد أفراد مجتمع البحث محدودا، كتلاميذ المستوى الأوّل في مدرسة معيّنة مثلا فإنه يمكن وضع أسمائهم على بطاقات، ثم وضعها في سلة وخلطها، وبعد ذلك، سحب العدد المراد من البطاقات، وأما إذا كانت الأعداد كبيرة، فإنه يتّم الاستعانة بجداول الارقام العشوائيّة التي نجدها في ملاحق كتب الإحصاء(المرجع السابق: 112)
2.1.2. العيّنة المنتظمة
يتّم اختيارها في حالة تجانس المجتمع الأصلي ولكن وفق ترتيب أو نظام معين، كأن نأخذ العيّنة من أصحاب الأرقام من مضاعفات عدد معيّن يحدده الباحث. وتُسمى عيّنة منتظمة لاختيار مسافة ثابتة وبانتظام بين كل رقم والرقم الذي يليه، ويمكن أخذ هذه العيّنة المنتظمة من المجتمع في حالة وجود قوائم لأفراده أو في حالة عدم توفر ذلك على سبيل المثال لو كان مجتمع الدراسة هو عدد التلاميذ الدارسين في شعبة علمي وعددهم 60 تلميذا المطلوب اختيار عينة عددها 12 تلميذا وبأسلوب العينة المنتظمة، ففي هذه الحالة يتم قسمة 60 على 12 فينتج 5 وتسمى بفترة المعاينة بعدها يتم اختيار رقم بشكل عشوائي ضمن الأرقام 1 5 ولنفرض أننا اخترنا الرقم 3 فيكون رقم المفردة الأولى ثم يضاف إليها الرقم 5 والذي يسمى (فترة المعاينة) والناتج نظيف له الرقم 5 وفي الأخير نستخرج العينة الآتية : [3-8-13-18-23-28-33-38-43-48-53-58]
تتميّز العيّنة العشوائيّة البسيطة في أن اختيارها يحدث بشكل أسرع لأنه لا يتطلب توّفر جدول الأعداد العشوائية وأنها أفضل تمثيلاً للمجتمع الأصلي من العيّنة العشوائيّة البسيطة.
3.1.2. العيّنة الإحصائيّة الطبقيّة
يتّم الاعتماد على هذه العيّنة بتقسيم المُجتمع الأصلي إلى طبقات أو فئات وفقا لخاصيّة معيّنة كالجنس أو المستوى التعليمي، فإذا كانت عناصر المجتمع غير متجانسة فإننا نقسّم المجتمع الى طبقات، ثم نأخذ عيّنة عشوائيّة بسيطة من كل طبقة تتناسب مع حجم الطبقة.
ويمكن توزيع العيّنة الطبقيّة الى:
-
توزيع متساوي وهنا نقسم العيّنة الكليّة على الطبقات بالتساوي.
-
توزيع متناسب/نسبي حيث يُوجد عدد من كل عيّنة يتناسب مع حجم الطبقّة في المجتمع. (النجار 2015: 96)
ويمكن الحصول على حجم العينة (i) من الطبقة (i) من خلال تطبيق القانون الاتي:
حيث أن:
-
:ni حجم العينة رقم (i)
-
Ni:حجم الطبقة (i)
-
N:حجم المجتمع الاحصائي.
-
n: حجم العينة المطلوب.
مثال: يراد اختيار عينة تتكون من 50 تلميذ من إحدى الثانويات، مع العلم أن عدد التلاميذ الإجمالي لهذه المؤسسة يتكون من 1000 تلميذ موزعين حسب المستوى، كما يلي :
-
400 تلميذ من شعبة الآداب.
-
300 تلميذ من شعبة علوم الطبيعة والحياة.
-
300 تلميذ ينتمون إلى شعبة الرياضيات.
لاحظ بأن المجتمع الإحصائي غير متجانس وبالتالي فإن أفضل طريقة لاختيار العينة هي العينة الطبقية. ولاختيار العينة المطلوبة نطبق القانون رقم(1) وذلك على النحو الاتي:
لدينا حجم المجتمع الإحصائي والذي يمثل العدد الإجمالي لتلاميذ المدرسة الثانوية 1000 N=،
-
50n=، حجم الطبقة الأولى 400 = 1N، حجم الطبقة الثانية 300 = 2N، حجم الطبقة الثالثة
-
300 = 3N
-
تطبيق عددي:
-
n1=400*50/1000, n1=20
-
n2=400*50/1000, n2=15
-
n3=400*50/1000, n3=15
ومنه تتضح العينة التي سوف نختارها، حيث سيتم اختيار عينة عشوائية من طلبة الآداب عددها 20 طالب، وعينة من شعبة علوم الطبيعة والحياة عددها 15 طالب وعينة من شعبة الرياضيات عدد 15 طالب أيضا.
4.1.2. العيّنة العنقوديّة
يختار الباحث العيّنة العنقوديّة من المجتمع الأصلي مُعتمداً على الاختيار العشوائي للوحدات وليس الأفراد حيث تكون لجميع الأفراد في هذه الوحدات خصائص مشابهة، ويُعتبر الاختيار بهذا الشكل أكثر ملائمة عندما يكون جمهور البحث كبيرا جداً أو منتشراً في مساحة جغرافيّة شاسعة. وتُعتبر مجموعة كاملة ذات خصائص متشابهة تجميعاً أو عنقوداً، فمثلا نأخذ غرف صفوف المدارس أو أحياء المدن الكبيرة وغيرها ونعتبرها كعناقيد، وبهذا يكون الاختيار العنقودي للعيّنة أسهل إن لم يكن أفضل من الاختيار العشوائي أو الاختيار الطبقي، ومن الممكن أن يتّم الاختيار العنقودي على مراحل ويسمى الاختيار متعدد المراحل، فقد نختار مثلاً المدارس لمدينة ما لإجراء دراسة ما بشكل عشوائي ثم نختار أيضاً بعض الصفوف على أساس عشوائي أيضاً، وبهذا تُعمم النتائج من العيّنة المختارة إلى الجمهور كله.
2.2. العيّنات غير العشوائيّة
وهي تلك العيّنات التي لا تضمن لجميع مفردات المجتمع احتمال ثابت ومحدد للاختيار وغالباً ما يتدخل الباحث في عملية الاختيار بصورة أو بأخرى، والتي يصعب فيها تحديد مجتمع الدراسة ومعرفة أفراده وعددهم، فيعمد في هذه الحالة الى اختيار مجموعة من المواصفات والمعايير التي وضعها والتي تفي بالغرض المنشود من الدارسة. ومثال على ذلك الدراسات حول الانحراف أو الادمان، ومن أهم أنواع العيّنات غير العشوائيّة ما يلي : العيّنة الغرضيّة، العيّنة القصديّة، العيّنة الحصصيّة وعيّنة كرة الثلج.
1.2.2. العيّنة الغرضيّة(القصديّة)
سُميّت هذه العيّنة بهذا الاسم نظرا لان الباحث يقوم باختيارها طبقا للغرض الذي يريد تحقيقه من خلال البحث، أي انه يختار العينة اختياراَ حراَ وفق حاجته وبحسب اعتقاده ورأيه الشخصي أن تلك العينة تمثل المجتمع وتحقق غرض دراسته، وبمعنى اخر يتم اختيارها على أساس توفر صفات محددة في مفردات العيّنة، وتكون تلك الخصائص من العناصر الهامة بالنسبة للدراسة. حيث يلجأ الباحث لمثل هذه العيّنات في حالة توافر المعطيات اللازمة للدراسة لدى فئة معيّنة من مجتمع الدراسة الاصلي، فمثلا لو أراد باحث دراسة الحياة الاقتصاديّة والاجتماعيّة للجزائريين ابان الحرب التحريريّة، فان ذلك يتطلب منه مقابلة الأفراد الذين عاشوا تلك الفترة. أي أن الباحث يختار أفراد العينة بشكل مدروس ومحدد وعن قصد).( قنديلجي 2009: 268)
2.2.2. العيّنة الحصصيّة
تُشبه العيّنة الحصصيّة العيّنة الطبقيّة من حيث المراحل الأولى في التحديد حيث يتم تقسيم مجتمع الدراسة الاصلي الى فئات أو شرائح ضمن معيار معيّن ثم يتم بعد ذلك اختيار العدد المطلوب من كل شريحة بشكل يتلاءم وظروف الباحث.
تعتمد هذه العيّنة على حصة(Quota) معيّنة من المجتمع الأصلي، بمعنى أن الباحث يختار نسبة معيّنة تمثل المجتمع الأصلي في مختلف خصائصه الكميّة والكيفيّة، وغالبا ما تكون هذه الحصة مئويّة. في هذا الإطار يرى عبد الكريم غريب بأنّ مقياس هذه العيّنة هو الاعتماد على معيار الحصة من فئة معيّنة، شأنها شأن العيّنة الطبقيّة،إلا أن عمليّة اختيار العيّنة الحصصيّة لا تكون عشوائيّة بل تُترك فيها الحريّة للباحث كي يتمكن من تحديد الحصّة التي يرغب فيها داخل كل فئة من الفئات. بمعنى أن العيّنة الحصصيّة تعتمد على معيار الحصة أو النسبة المئويّة في رصد البيانات والمعطيات. (غريب 2012: 175)
مثال: قد يظن أن اتجاهات العمال نحو العمل في المنظمة تختلف كثيرا عن اتجاهات الموظفين نحو العمل بالمنظمة أيضا، فإذا كان عدد العمال 60% وعدد الموظفين 40 %، وإذا كان الباحث بصدد مقابلة 30 من العمال والموظفين ليحصل على إجابة لسؤال البحث الخاص بمدى الاختلاف بين اتجاهات المجموعتين، فإن حصة العمال في هذه العيّنة 18 عاملا وحصة الموظفين 12 موظفا، وذلك لأن هذه الأرقام تشكل 60% و40% من العيّنة.
3.2.2. عيّنة الصدفة
يختار الباحث عددا من الافراد الذين يُقابلهم بالصدفة دون تخطيط كأن يختار كل من يمر في منطقة معيّنة أو خلال ساعة معيّنة، أو كأن يذهب الباحث الى مكتبة معيّنة أو مدرسة أو كليّة من الكليّات التي يتعلق البحث بها، حيث يوزع الاستمارة على من يجدهم أمامه ليأخذ رأيهم في موقف أو قضيّة ما، ويضطر العديد من الباحثين الى اعتماد هذا النوع من العيّنة لسهولة استخدامها وربما لضيق الوقت لديه أو أي مبرر أخر، ومن أبرز سلبياتها أنها قد لا تمثل المجتمع الأصلي تمثيلاً صادقاً خاصة إذا كان هناك تباين أو عدم تجانس في الخواص أو الصفات الموجودة في المجتمع الأصلي، كذلك قد يواجه الباحث في هذه العيّنات مشكلة عدم استجابة بعض الافراد الذين يختارهم في العيّنة وذلك الى حساسيّة بعض الاستمارة المستخدمة في جمع البيانات أو بسبب فقدان الاهتمام بموضوع الدراسة. ( الدليمي 2004: 64)
4.2.2. عيّنة كرة الثلج
تستخدم هذه الطريقة غالبا للحصول على عيّنة عندما لا تتوّفر قائمة معلومة يمكن استخدامها كإطار للعيّنة، وكما تعتبر طريقة للحصول على عيّنة من الجماعات التي تمارس سلوكا غير سويّ مثال: متعاطي المخدرات، المشردين... الخ.
في مثل هذه الوضعيّة يطلب الباحث من المشارك ان يقترح مشارك اخر أو أكثر تنطبق عليهم تلك الصفات لكي يكونوا ضمن العيّنة. وبمعنى اخر الاتصال بطرف الخيط من خلال شخص وبعدها يتّم الوصول من واحد إلى الآخر حيث تكبر العيّنة مع تقدم البحث أي تكبر كرّة الثلج. ويعاب على هذه الطريقة أنها لا تمثل المجتمع تمثيلا دقيقا، ولكنها مفيدة في الحالات التي يصعب الوصول فيها إلى أفراد مجتمع الدراسة ( بن جخدل 2019: 66)
3. الاختبارات الإحصائيّة
المعلم (paramétrique) مفردة وتعني صفة أو خاصية لمجتمع معين في مقابل تقدير (estimateur) التي يكون صفة أو خاصية لعينة ما، وأهم ما يميّز الاسلوب المعلمي عن الاسلوب اللامعلمي هو الوسط الحسابي والانحراف المعياري ولذلك يميز علم الاحصاء بين شروط اختبار(ت) للعينات المستقلة و(ت) للعينات المترابطة لأن الاسلوب اللامعلمي لا يتعامل مع الاوساط والانحرافات بينما نجد ان اختبار(ت) للعينات المستقلة يتعامل معها اسوة بقوانين تحليل التباين (F) وقوانين (Z)، من هنا يمكن القول أن الأسلوب المعلمي هو مجموعة من الطرق التي تشترط تحقق افتراضات محددة حول المجتمع الذي تسحب منه العينة وهنا مقتضى الدقة الانتباه للتعبير (حول المجتمع) كونه يختلف عن (العينة) ولذلك فان الاسلوب اللامعلمي هو مجموعة من الطرق البديلة التي تستخدم في حالات عدم تحقق الافتراضات حول المجتمع الذي تسحب منه العينة، أو في حالة البيانات الاسمية والرتبية وكلا الأسلوبين(المعلمي،اللامعلمي) من أقسام الاحصاء الاستدلالي التي يمكن تعميم نتائجها على المجتمع، إلا أن لكل منها مستوى ثقة معين يتحدد على ضوء المعطيات المتوفرة.
1.3. الاختبارات المعلميّة
تعتبر الاختبارات المعمليّة من الاختبارات الإحصائيّة الأشهر والأكثر استخداماً، حيث تستعمل كافة المعلومات والبيانات وبالتالي لديها الإمكانية في الوصول إلى نتائج أكثر وأكبر، وتُجرى عادة على البيانات التي تتوزع توزيعا طبيعيا ومن أهمها اختبار T فضلا عن اختبارات أخرى التي تستعمل في حالة المقارنات المتعددة، حيث أن تطبيقها على البيانات التي تتوزع توزيعا طبيعيا سيعطي نتائج غير دقيقة.
2.3. الاختبارات اللامعلميّة
تختبر فروضا لا تتعلق بمعالم المجتمع، ولكن تتعلق بأشياء أخرى، قد تكون وصفيّة مثل العلاقة هي الاختبارات التي لا تُبنى على أساس التوزيع الطبيعي للبيانات، بينما تُبنى على بيانات عشوائيّة التوزيع، مثل البيانات الاسميّة، ولا يستخدم الباحث جميع المعلومات والبيانات التي حصل عليها من أفراد العيّنة كما في اختبارات التحليل الإحصائي المعلميّة، ولذلك لا يمكنه أن يكتشف جميع العلاقات والفروق الإحصائية، بين التعليم والتدخين، والعلاقة بين لون العينين ولون الشعر وفي هذه الحالة يسمى الاختبار باسم الاختبار اللامعلمي (النجار 2015: 351)
4. الفروض الإحصائيّة مستوى الدلالة الإحصائيّة ومنطقة الرفض
1.4. الفروض الإحصائيّة
هي بمثابة اقتراح لمعالم المجتمع محل الدراسة والتي مازالت غير معلومة للباحث فهي إذن حلولا ممكنة لمشكلة البحث، وهي نوعان:
-
فرض العدم (الفرضيّة الصفريّة) ويرمز لها بالرمز H0، وكلمة عدم تدل على أنه لا يوجد فرق بين معلمة المجتمع والقيمة المدعاة (إحصائيّة العيّنة).
-
الفرض البديل ويرمز لها بالرمز H1، وهي التي يضعها الباحث كبديل عن فرض العدم ونقبلها عندما نرفض فرض العدم باعتبارها غير صحيحة بناءا على المعطيات المستقاة من العيّنة.
وعند اجراء اختبارات الفروض يمكن الوقوع في خطأين1:
-
الخطأ من النوع الأول: هو رفض فرض العدم وهو صحيح، ويرمز له بالرمز α
-
الخطأ من النوع الثاني: هو قبول فرض العدم بينما هو خاطئ، ويرمز له بالرمز
2.4. مستوى الدلالة الإحصائيّة ومنطقة الرفض
عندما نقبل الفرضية الصفرية (فرض العدم) فإننا نقبلها بنسبة دقّة 95 أو 99 أو غير ذلك، وتسمى مستويات الدلالة أو الثّقة أي يوجد نسبة خطأ معيّن في قبولنا للفرضيّة الصفريّة وهي خاطئة وهذا الخطأ هو α ويسمى مستوى المعنويّة.
إذا كان مستوى الثقة 95 1-α،فإن مستوى المعنويّة α تساوي 5 وهي عبارة عن مساحة المنطقة التي تقع تحت منحنى التوزيع والتي تمثل منطقة الرفض، وتكون من طرف واحد إما على صورة ذيل واحد جهة اليمين أو اليسار أو من طرفين (ذيلين متساويين في المساحة واحد على جهة اليمين والأخر على اليسار، وفي هذه الحالة يتم تقسيم /2). ( كفروني 2011: 65)
5. استخدام الاختبارات اللابارميتريّة(اللامعلمية) : اختبار كاي مربع (كا2
تُستخدم الاختبارات اللابارميتريّة كثيرا في مجال العلوم الإنسانية والاجتماعية وذلك لأنها تناسب بدرجة كبيرة وطبيعة الظواهر والمتغيرات ولا يتطلب أية افتراضات أو معلومات حول خصائص التوزيع الأساسي للمجتمع، وهو أكثر ملائمة لمعالجة وتحليل البيانات من المستوى الاسمي والرتبي (المتغيرات النوعية)، تستخدم في حالة العيّنات غير عشوائيّة، ومن أهمها:
يستخدم كا2 أساسا في قياس مدى التطابق بين توزيعين أحدهما توزيع فعلي لمتغيّر تم قياسه والأخر توزيع نظري أو متوّقع، وعلى ذلك فوجه المقارنة يكون بين مجموعتين من البيانات التكراريّة إحداهما فعليّة والأخرى نظريّة ويكون الغرض من الموضوع هو المتعلق بالفروق أو الاختلافات بين التوزيعات الفعليّة أو المشاهدة، والتوزيعات المتوّقعة للوقوف على معرفة نوع هذه الفروق، هل فروق معنويّة أم أنها جوهريّة، أم أنها مجرد فروق ظاهريّة ؟ فإذا كانت الفروق حقيقيّة فذلك يعني أنها نتيجة لعوامل مسؤولة عنها وليست مرتبطة بعوامل أخرى مسبّبة لها، أما إذا كانت غير جوهريّة، فإن ذلك يعني أنها نتيجة للصدفة. ( البدري 2014: 173)
يُعتبر اختبار الاستقلاليّة كاي مربع من المقاييس اللابراميتريّة ولتطبيقه يجب مراعاة الشروط الآتية:
-
في حالة الجداول من النوع 2*2 يجب أن لا تقّل أية قيمة نظريّة أقل من 5.
-
في حالة الجداول من النوع أكبر من 2*2 فإن: قيّم خلايا الجدول لا يجب أن تكون أي خليّة من خلايا الجدول أقل من الواحد، ولا يجوز أن تتعدى 20% القيّم الأقل من 5 وفي حالة وجود قيمة أقل من 5 يجب دمج العمود الذي تتواجد فيه هذه القيمة في العمود الذي قبله أو الذي يليه، أو الصف الذي قبله أو الذي يليه.
وفي حالة توّفر هذه الشروط يشرع في تطبيق اختبار كا2 وفق المراحل الآتية:
1.5. صياغة الفروض
هناك نوعان من الفروض، الفرض الصفري (فرض العدم) والفرض البديل، والذي يفترض عدم وجود علاقة بين المتغيرين، ويتم صياغته كما يلي:
-
فرض العدم(H0): لا توجد علاقة بين المتغيّر المستقل والمتغيّر التابع.
-
فرض العدم(H1): توجد علاقة بين المتغيّر المستقل والمتغيّر التابع.
ولقبول أو رفض الفرض الصفريّ نتبع الخطوات الآتية : نقوم بحساب كا2 المحسوبة وفق القانون التالي:
مع العلم أن القيّم المتوّقعة يمكن حسابها وفق القانون الاتي:
نقوم بحساب كاي مربع الجدوليّة انطلاقا من تحديد مجال الثقة : 95%، 99% ودرجة حريّة =(عدد الاعمدة-1) (عدد الصفوف-1)
2.5. قاعدة القرار
عندما تكون كا2 المحسوبة أكبر من كا2 الجدوليّة نرفض فرض العدم، ونقبل الفرض البديل أي توجد علاقة بين المتغيرين.
وللتذكير فإن الأهم هو رفض فرض العدم عند مستوى المعنويّة 0.01، وفي هذه الحالة لا نكتفي فقط بالقول أن هناك علاقة بل يجب التحري عن طبيعة هذه العلاقة، وبعبارة أخرى هل هذه العلاقة ضعيفة ؟ متوسطة ؟ أم قوية ؟ وللإجابة على هذه الاشكالية، نتبع الإجراءات الآتية:
-
في حالة الجدول المزدوج 2*2 بمتغيرات إسميّة: نعتمد مقياس العلاقة (في)
-
في حالة الجدول المزدوج أكبر من 2*2 بمتغيرات إسميّة: نعتمد على العلاقة كرامر(V) وفق الصيغة الآتية :
مع العلم أن:K=العدد الأصغر في الصفوف أو الأعمدة.
نستخدم هذه المقاييس لتحديد قوة العلاقة أو الارتباط بين المتغيرات الاسمية والتي تتراوح ما بين0-1 وذلك وفقا لنتائج الارتباط الآتية:( كفروني 2011: 65)
الجدول 02:يبين دلالة الارتباط للمتغيرات الإسمية.
|
دلالة الارتباط للمتغيرات الإسميّة: |
0.25 وأكبر |
0.15-0.25 علاقة قويّة |
|
0.11-0.15 علاقة متوّسطة |
0.06-0.11 علاقة ضعيفة |
0.01-0.06 لا علاقة |
االمصدر: يوسف كفروني، (2011)، ص65:
أما فيما يخص المتغيّرات الرُّتَبية فالأمر يختلف عن الإجراء السابق الذي ذكرناه في حالة المتغيّرات الإسميّة، حيث يتوّجب علينا تطبيق معامل ارتباط غاما وفق العلاقة الآتية:
6 كيفية قراءة الجداول
قبل الخوض في كيفيّة قراءة الجداول يتوّجب علينا أن نشير إلى ماهية الجدول المزدوج وهو نوع من الجداول الذي يحتوي على متغيرين أحدهما مستقل والأخر تابع أو يحمل متغيرين يتبادلان الأدوار، وهي الجداول التي غالبا ما تُستعمل في اختبار الفروض، سواء كانت هذه الاختبارات معلميّة أو لامعلميّة.
ومن أهم الخطوات المتبعة في قراءة الجداول ما يلي:
-
نبدأ أولا بالقراءة الشاملة ثم ننتقل إلى القراءة الأفقيّة والقراءة العموديّة، ونادرا ما نلجأ إلى قراءة النسبة المئوية الكليّة، فقد نكتفي بالإشارة إلى أبرز النسب فيها.
-
عندما يكون المتغيّر الأفقي مستقلا والمتغيّر العمودي تابعا ولا يمكن أن يتبادلا الأدوار وتكون القراءة الأفقيّة اضافة إلى القراءة الشاملة كافيّة ومعبّرة.
-
في القراءة الشاملة نستعرض واقع العيّنة الإجمالي(العدد الكلي، الفئات التي يتوزع عليها كل متغير، مجموع كل فئة من فئات المتغيّر الأفقي وفئات المتغيّر العمودي ونسبته المئويّة من المجموع الكلي).
-
في القراءة الأفقيّة، نستعرض مجموع كل فئة من فئات المتغيّر الأفقي وكيفية توزعه على مختلف فئات المتغيّر العمودي.
-
نجري مقارنة بين فئات المتغيّر الأفقي لنرى إن كان هناك اختلاف في طريقة التوزع على فئات المتغيّر العمودي، ونعتمد في المقارنة على النسب المئويّة الأفقيّة.
-
في القراءة العمودية: نستعرض مجموع كل فئة من فئات المتغير العمودي وكيفية توزعه على مختلف فئات هذا المتغيّر، ثم نُجري مقارنة بين فئاته ( المتغيّر العمودي) لنرى إذا كان هناك اختلاف في طريقة التوّزع على فئات المتغيّر الأفقي، ونعتمد في المقارنة على النسب المئويّة العموديّة( كفروني 2011: 60)
7. التمثيل البياني
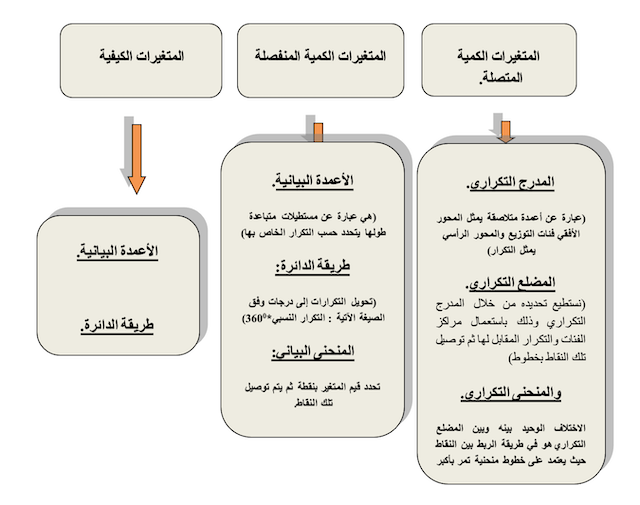
تُستعمل الاشكال البيانيّة لتفسير تطوّر الظواهر وتوزيعها ومن مميّزاتها سهولة قراءتها حتى من طرف الأشخاص غير المختصين، وفي هذا الإطار لاحظنا في بعض مذكرات التخرج وجود بعض الأخطاء فيما يخص اختيار الاشكال البيانيّة المناسبة، ولهذا الغرض سوف نتطرق للضوابط التي تحكم استخدام تلك الرسومات وفق المتغيّرات التي نُريد تمثيلها وبما أن البيانات نوعان: كميّة تعبر عن قيمها بالكّم وتنقسم إلى قسمين كميّة متّصلة تقبل التجزئة أي أنها تُعبر عن قيّمها بالفاصلة (كالأطوال، الأوزان والأحجام...) وكميّة منفصلة تعبّر عن قيّمها بأعداد صحيحة(عدد أفراد الأسرة، عدد الطلبة داخل القسم...) وبيانات كيفيّة تقاس بمعيار إسمي مثل(الجنس : ذكر، أنثى والحالة العائليّةـ والجنسيّة والديّانة...) وبيانات كيفيّة تُقاس بمعيار رتبي أو سلمي (المستوى التعليمي، تقدير العلامات، جودة منتوج معين)، حيث سنتطرق إلى التمثيل البياني المناسب لكل نوع من أنواع البيانات السالفة الذكر وفق الشكل الاتي:
الشكل رقم 2 : أنواع المتغيرات والتمثيل البياني المناسب.
المصدر: مجهود شخصي
الخاتمة
يُعتبر أسلوب التحليل الإحصائي من الأساليب التي يتم استخدامها في جميع أنواع الدراسات والتخصصات، حيث يُسهل كيفيّة جمع البيانات وفق الشروط العلميّة للتوّصل الى تفسير، توضيح وفهم العديد من الظواهر والمشكلات الغامضة، بالإضافة إلى قدرته على القيام بالتنبؤ العلمي في المستقبل، وكما يعتبر أسلوب التحليل الإحصائي من الطرق التي تستخدم في البحوث العلمية، اذ تتميّز بدّقة النتائج التي تقدمها، بشرط أن يُجيد الباحث استخدام هذه الخطوات والشروط، وأن يكون على علم بها، حيث يتّطلب استخدام هذه البرامج الدراية الكاملة بها وبكيفيّة استخدامها. وفي الختام نرجو أن نكون قد وُفقنا في تقديم الخطوات والشروحات حول أسلوب التحليل الإحصائي، حيث يساعد الباحث للوصول إلى نتائج دقيقة عند دراسته لمختلف المواضيع والظواهر وخاصة إذا استعان بمختلف الحزم الاحصائية المتوفرة، وعليه نقترح التوصيات الآتية:
-
الحرص على اختيار عينة مناسبة حتى يتسنى تعميم النتائج على المجتمع.
-
استخدام الجداول المركبة لإجراء الاختبارات الإحصائية التي تبين لنا طبيعة العلاقة بين المتغيرات.
-
قراءة الجداول الاحصائية بشكل صحيح مع دعمها بأشكال بيانية مناسبة.
-
4-التمثيل البياني ليس عملية عشوائية، بل يخضع لقواعد مفادها أن لكل نوع من البيانات (كمية، أو كيفية) تمثيلها البياني الخاص بها.